How To Use Parametric And Nonparametric Variables In Data Modeling
It'south rubber to say that most people who use statistics are more than familiar with parametric analyses than nonparametric analyses. Nonparametric tests are also called distribution-free tests because they don't assume that your data follow a specific distribution. You may take heard that you should use nonparametric tests when your data don't run across the assumptions of the parametric test, especially the assumption most normally distributed information. That sounds like a dainty and straightforward way to choose, but there are additional considerations. In this post, I'll assist yous determine when you should utilize a: In detail, I'll focus on an important reason to utilise nonparametric tests that I don't think gets mentioned often enough! Nonparametric tests are similar a parallel universe to parametric tests. The table shows related pairs of hypothesis tests that Minitab Statistical Software offers. Parametric tests (means) Nonparametric tests (medians) 1-sample t examination 1-sample Sign, 1-sample Wilcoxon ii-sample t exam Mann-Whitney test I-Way ANOVA Kruskal-Wallis, Mood's median test Factorial DOE with i cistron and one blocking variable Friedman test Reason 1: Parametric tests can perform well with skewed and nonnormal distributions This may exist a surprise but parametric tests tin can perform well with continuous data that are nonnormal if you satisfy the sample size guidelines in the table below. These guidelines are based on simulation studies conducted past statisticians here at Minitab. To learn more about these studies, read our Technical Papers. Parametric analyses Sample size guidelines for nonnormal data one-sample t examination Greater than 20 2-sample t test Each grouping should exist greater than 15 One-Way ANOVA Reason two: Parametric tests can perform well when the spread of each group is different While nonparametric tests don't assume that your data follow a normal distribution, they practise have other assumptions that can be hard to meet. For nonparametric tests that compare groups, a common assumption is that the data for all groups must have the aforementioned spread (dispersion). If your groups have a different spread, the nonparametric tests might not provide valid results. On the other hand, if you utilize the 2-sample t test or Ane-Way ANOVA, you can but go to the Options subdialog and uncheck Assume equal variances. Voilà, you're good to get even when the groups accept unlike spreads! Reason 3: Statistical power Parametric tests usually take more statistical power than nonparametric tests. Thus, you lot are more probable to detect a significant consequence when one truly exists. Reason 1: Your area of study is meliorate represented by the median For example, the center of a skewed distribution, like income, tin can be better measured by the median where 50% are above the median and 50% are below. If you add a few billionaires to a sample, the mathematical mean increases greatly even though the income for the typical person doesn't change. When your distribution is skewed plenty, the mean is strongly affected by changes far out in the distribution's tail whereas the median continues to more closely reverberate the center of the distribution. For these two distributions, a random sample of 100 from each distribution produces means that are significantly dissimilar, just medians that are not significantly different. 2 other blog posts illustrate this bespeak well: Reason 2: You accept a very small sample size If y'all don't meet the sample size guidelines for the parametric tests and you are not confident that you have normally distributed data, you should use a nonparametric test. When y'all have a really small sample, you might not fifty-fifty be able to ascertain the distribution of your information because the distribution tests will lack sufficient power to provide meaningful results. In this scenario, y'all're in a tough spot with no valid alternative. Nonparametric tests have less ability to begin with and it's a double whammy when you add together a small-scale sample size on top of that! Reason iii: You lot have ordinal information, ranked information, or outliers that you lot can't remove Typical parametric tests tin can just assess continuous data and the results tin can be significantly afflicted by outliers. Conversely, some nonparametric tests can handle ordinal data, ranked data, and not be seriously affected by outliers. Be sure to cheque the assumptions for the nonparametric exam because each i has its own information requirements. If you have Likert data and want to compare two groups, read my post Best Way to Clarify Likert Detail Data: 2 Sample T-Test versus Mann-Whitney. Information technology's commonly thought that the need to choose between a parametric and nonparametric test occurs when your data neglect to run across an assumption of the parametric test. This can exist the case when you have both a modest sample size and nonnormal data. Even so, other considerations often play a part because parametric tests tin ofttimes handle nonnormal data. Conversely, nonparametric tests accept strict assumptions that you can't disregard. The decision frequently depends on whether the mean or median more than accurately represents the centre of your information's distribution. Finally, if you have a very small sample size, you lot might be stuck using a nonparametric test. Please, collect more data next time if it is at all possible! As you lot tin see, the sample size guidelines aren't really that large. Your chance of detecting a pregnant effect when one exists can be very minor when you have both a small sample size and yous need to utilize a less efficient nonparametric examination!
Hypothesis Tests of the Mean and Median
Reasons to Use Parametric Tests

Reasons to Use Nonparametric Tests
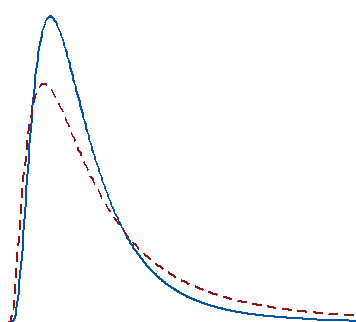 This is my favorite reason to use a nonparametric test and the one that isn't mentioned often enough! The fact that you can perform a parametric test with nonnormal data doesn't imply that the mean is the statistic that y'all desire to test.
This is my favorite reason to use a nonparametric test and the one that isn't mentioned often enough! The fact that you can perform a parametric test with nonnormal data doesn't imply that the mean is the statistic that y'all desire to test.
Endmost Thoughts
How To Use Parametric And Nonparametric Variables In Data Modeling,
Source: https://blog.minitab.com/en/adventures-in-statistics-2/choosing-between-a-nonparametric-test-and-a-parametric-test
Posted by: crowprieture.blogspot.com


0 Response to "How To Use Parametric And Nonparametric Variables In Data Modeling"
Post a Comment